Compounding Interest; Consider the following scenario…

If you put $1,000 into a savings account at 3% annual interest. At the end of 2 years, your balance won’t be $1,060 ($1,000 principal + $30 interest each year). You will have a little more than that.

You will have $1,060.90. This is because in Year 2 you earn interest on more than the original $1,000.

At the end of Year 1, you will have $1,030. Thus, in Year 2 you earn 3% interest on $1,030, not $1,000. This is the magic of compounding interest: you earn interest on both the original principal and previously-earned interest that’s added to the principal.

Of course, in the real world the simple example I just gave isn’t quite accurate. In practice, different banks compound interest at different intervals, usually on a daily, monthly, or quarterly basis.

The more frequently the bank compounds interest, the better it is for you. The more frequently you are credited for the interest, the higher is your annual percentage yield (APY), the effective rate of return for the year.

If your bank compounds interest daily, the bank credits your account with 1/365 of the interest rate every day. In this case, compounding interest increases the value of your account every day.

If your bank compounds interest monthly, the bank credits your account with 1/12 of the interest rate every month. The compounding increases the value of your account every month. For quarterly compounding, it would be 1/4 of the interest rate.

Let’s calculate how the APY changes when a bank that pays 3% annual interest rate compounds every month.

The APY formula is (1 + R/N)N – 1. R is the interest rate and N is the number of compounding periods per year.

So in our example, the APY is calculated as (1 + 0.03/12)12 – 1, or 3.0416%. Obviously, this is higher than the 3% annual rate.

The difference is small, but it’s still a difference. If the interest rate was higher, then the difference caused by compounding would be larger.

The accompanying table shows how the value of $1,000 would grow at monthly compounding.

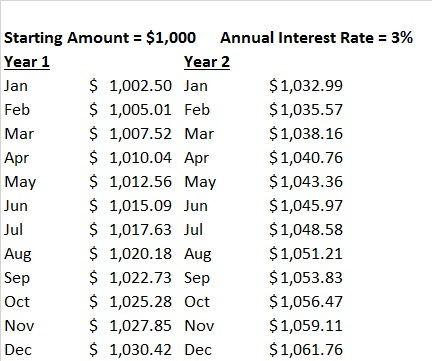
Compounding interest comes into play in stock investing as well.

One example would be dividend reinvestment. If you reinvested in a publicly-traded company’s DRIP (dividend reinvestment plan), every time the company pays a dividend, the dividend would automatically be used to purchase additional shares of that company’s stock commission-free.

Over time, because you will have more and more shares of the stock, you receive more cash dividend, which then would purchase more shares, and when the stock price rises, in dollar terms you also gain more. It becomes a virtuous cycle.

To examine the compounding effect of DRIP, let’s consider a hypothetical example:

Let’s say 10 years ago you invested $5,000 in 100 shares of XYZ stock. XYZ pays $3 per share in dividend annually. The dividend doesn’t grow, but the stock price grows at an annual rate of 5%. At the end of 10 years how big a difference would DRIP make?

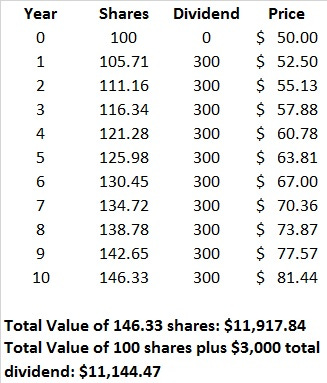
If you participated in XYZ’s DRIP, at the end of 10 years that $5,000 would have turned into $11,917.84 and you would own 146.33 shares of XYZ.

If instead you just kept the dividend in cash, your total investment, including the dividend received, would be worth $11,144.47, or 6.5% lower than the DRIP scenario. Of course, if you were able to invest the cash dividend in something that has an even greater return, you would beat the return of the DRIP scenario, but that’s a big if.

A word of caution: if XYZ falls in price, the compounding effect of DRIP could increase the size of the loss. However, since historically stocks rise in value, the net compounding effect of DRIP will likely be positive.

Sharing is Caring. Feel free to share this article with a friend or fellow investor.